The Chemist Volume 88 | Number 1
ISSN 1945-0702
Discovering Infinite Number of Independent Balanced Forms of Some Typical Chemical Equations Pramode Ranjan Bhattacharjee Kabi Nazrul Mahavidyalaya, Sonamura | West Tripura, Pin – 799 131, India (E-mail: drpramode@rediffmail.com)
Abstract: This paper reports on a novel idea falling within the purview of chemical science and engineering. It deals with a novel procedure for the algebraic method of balancing chemical reaction equations. The basic principle and relevant procedure of the novel scheme are offered along with illustrative examples. The fact that the balanced form of a chemical equation is not always unique is illustrated by the novel procedure offered in the paper. It has been found from the present study that, for each of the chemical equations (not involving ions) with {(m + n) – s} > 1, and for each of those involving ions with {(m + n) – s} > 2, where m = total number of reactants, n = total number of products, and s = total number of different kinds of elements on each side of the chemical equation, there exists an infinite number of independent balanced forms for each of those typical chemical equations. Key Words: Chemical reaction; Chemical equation; Balancing of chemical equation.

Introduction

Chemical equations are widely used in theory and practice. It is well known that the elements and compounds are expressed by their symbols and formulae, respectively. The chemists have devised a shorthand method to represent a chemical reaction symbolically, instead of in words. Such a shorthand method of representation of a chemical reaction with the help of symbols and formulae is called a chemical equation. If both the qualitative, as well as the quantitative, aspects of the reaction are reflected by a chemical equation, the equation is said to be a true, or correct, or balanced chemical equation. On the other hand, if a chemical equation only reflects the qualitative aspect of the chemical reaction, the equation is said to be an unbalanced chemical equation. A balanced chemical equation also helps in forming a mental picture in regard to the physical nature and properties of the reactants (viz., colour, state, etc.), as well as the chemical result and its physical nature. Balancing of chemical equations is an essential part of chemical mathematics called Stoichiometry, that is concerned with the mass and mole relationships determined by chemical equations and formulae. For these reasons, writing down a chemical equation correctly has drawn much attention in Chemical Education Research [1,13]. Chemistry students ought to be well conversant in writing and balancing chemical equations. The balancing of chemical equations is also an excellent exercise from demonstrative as well as pedagogical points of view.

This paper concentrates on the algebraic method of balancing chemical equations. The usual procedure of balancing chemical equations in the algebraic method is based on the fundamental principles of conservation of mass and charge. According to the principle of conservation of mass, the quantity of each element must remain the same on both sides in a chemical reaction. Thus, the same quantity of each element must appear on both sides of the true or balanced chemical equation. Also, from the principle of conservation of charge, the charge must be conserved in a chemical reaction. So, the same charge must remain present on both sides of the balanced chemical equation. Balanced equations are to be written with the smallest integer coefficients. If the coefficient is 1, it is understood.

The underlying principle as well as the procedure of the algebraic method of balancing chemical equation has been explained first in a novel way, considering a few examples. After applying this procedure to typical chemical equations, it is possible to generate an infinite number of independent balanced forms for each of those chemical equations without inviting any kind of ambiguity.

Thus, the present work enhancing the efficiency of the algebraic method of balancing chemical equations deserves special attention to the scientific and engineering community.

Basic Principles Involved in the Algebraic Method of Balancing Chemical Equations

Let us consider the chemical equation:

R₁ + R₂ + R₃ + … + R_m  →  P₁ + P₂ + P₃ + … + P_n  … (1)

with “m” number of reactants and “n” number of products.  Let the number of different kinds of elements on each side of this chemical equation be “s”.  The balanced form of this chemical equation may be written as:

( c₁ ) R₁ + ( c₂ ) R₂ + ( c₃ ) R₃ +  …  + ( c_m )R_m →  (C_m+1)P₁ + (C_m+2)P₂ + (C_m+3)P₃ + … + (C_m+n)P_n… (2)

where the (m + n) coefficients c₁, c₂, c₃,  …  , c_m, c_m+1, c_m+2, c_m+3, … , c_m+n are smallest possible positive integers.

Since equation (2) is a balanced form of the chemical equation, the total number of each kind of the “s” number of elements on both sides of equation (2) must be equal. Equating the total number of each kind of “s” elements on both sides of equation (2), it would then be possible to write down a total of “s” linear equations involving the coefficients c₁, c₂, c₃, … , c_m, c_m+1, c_m+2, c_m+3,... , c_m+n.

It may now be noted that each of the aforesaid “s’ number of equations will remain unchanged if both sides of each of those “s” number of equations are multiplied by µ (where µ is a constant or a positive integer or a non-negative proper fraction). Thus the aforesaid “s” equations  will then be changed to “s” number of other linear equations involving the coefficients x₁, x₂, x₃, … , x_m, x_m+1, x_m+2, x_m+3, … , x_{m+ n}, where  x₁ = µc₁, x₂ = µc₂, x₃ = µc₃, … , x_m = µc_m, x _m+1 = µ _m+1 , x _m+2 = µ _m+2, x _m+3 = µ _m+3, … , x _{m+ n} = µ _m+n.

It may further be noted that:

x₁ : x₂ : x₃ : … : x_m : x_m+1 : x_m+2 : x_m+3 : … : x_{m+ n} = c₁ : c₂ : c₃ : … : c_m : c_m+1 : c_m+2 : c_m+3 : … : c_{m+ n},
where c₁, c₂, c₃, … , c_m, c_m+1, c_m+2, c_m+3, … , c_m+n are smallest possible positive integers.

Thus, to find the balanced form of a chemical equation of the type represented by equation (1) above, we should consider the “s” number of linear equations involving the (m + n) coefficients, x₁, x₂, x₃, …, x_m, x_m+1, x_m+2, x_m+3, … , x_{m+ n}, where  x_i= µc_i , i  ε { 1, 2, 3, … , m, m + 1, m + 2,  m + 3, … ,  m + n }.

Those “s” number of equations are to be employed to ultimately find the ratio  x₁ : x₂ : x₃ : … : x_m : x_m+1 : x_m+2 : x_m+3 : … : x_m+n  in the simplest possible positive integer form, c₁ : c₂ : c₃ : … : c_m : c_m+1 : c_m+2 : c_m+3 : … : c_{m+ n},  with a view to identifying the required coefficients, c₁, c₂, c₃, … , c_m, c_m+1, c_m+2, c_m+3, … , c_{m+ n}, with the help of which the balanced form(s) of the chemical equation under consideration could be easily written.

If the chemical equation under consideration contains ions, one more linear equation that will result from the conservation of charge is to be considered. In such a case there will be in all (s +1) equations involving the coefficients xi s, where  x_i = µc_i, i ε { 1, 2, 3, … , m, m + 1, m + 2,  m + 3, … , m + n }. Those (s +1) equations will then be considered as above to pick out the required coefficients, c₁, c₂, c₃, … , c_m, c_m+1, c_m+2, c_m+3, … , c_m+n, in order to write down the balanced form(s) of such a chemical equation.

The Novel General Procedure of Balancing Chemical Equations by Algebraic Method

The novel general procedure of balancing chemical reaction equation by algebraic method to be considered in this paper is based on the principle of conservation of mass as well as the principle of conservation of charge like the traditional schemes. The procedure of balancing a chemical equation in the novel approach is based on the following steps.

Step 1: Write the chemical reaction equation using the coefficients x_i s, where i ε { 1, 2, 3, 4, 5, 6, 7, … , m + n}, “m” and “n” being respectively the total number of reactants and that of the products of the relevant chemical reaction.

Step 2: Form a set of “s” linear equations involving the coefficients x_i s by equating the total number of element of each kind on both sides of the chemical equation, where “s” is the total number of different kinds of elements on each side of the chemical equation under consideration.

Step 3: If charged molecules or/and ions remain present in the chemical equation, form the (s + 1)th linear equation involving the coefficients x_i s by equating the total charge on both sides of the chemical reaction equation.

Step 4: Consider all the equations formed in Step 2 and Step 3.

Step 5: By choosing any one of the coefficients x_i to be equal to k₁, where k₁ is a positive integer or a non-negative proper fraction, see whether it is possible to express all other remaining coefficients x_i s in terms of k₁. If so, continue on to Step 6. Otherwise, go to Step 8.

Step 6: Express the ratio x₁ : x₂ : x₃ : … : x_m+n in the simplest possible positive integer form c₁ : c₂ : c₃ : … : c_{m+ n}, and identify the corresponding values of the coefficients c_i s , i ε { 1, 2, 3, … , m + n }.

Step 7: Use the values of the coefficients, c₁, c₂, c₃, … , c_m+n obtained in Step 6 to write down the only one balanced form of the relevant chemical equation.

Step 8: If by choosing the value of a particular coefficient x_i to be equal to k₁, where k₁ is a positive integer or a non-negative proper fraction, it is not possible to express all other remaining coefficients x_i s in terms of k₁, choose a second coefficient x_i to be equal to k₂, where k₂ is a positive integer or a non-negative proper fraction, and see whether the remaining (m + n − 2) coefficients xi s can be expressed in terms of k₁ and k₂. If so, continue on to Step 9. Otherwise, go to Step 13.

Step 9: Remembering that each of k₁ and k₂ may be a positive integer or a non-negative proper fraction, assign any one of such pair of values to k₁ and k₂ out of the infinite number of choices and find the values of all the coefficients x_i s, i ε { 1, 2, 3, … , m + n }.

Step 10: Express the ratio x₁ : x₂ : x₃ : … : x_m+n in the simplest possible positive integer form, c₁ : c₂ : c₃ : … : c_m+n, and identify the corresponding values of the coefficients c_i s, i ε { 1, 2, 3, … , m + n }.

Step 11: Use the values of the coefficients, c₁, c₂, c₃, … , c_m+n obtained in Step 10 to write down one balanced form of the relevant chemical equation for the particular choice of the values of k₁ and k₂ as made in Step 9.

Step 12: Repeat Step 9 to Step 11 for each and every other pair of values of k₁ and k₂ out of an infinite number of choices to derive the corresponding other independent balanced forms of the chemical equation under consideration.

Step 13: Repeat Step 8 to Step 12 by choosing a third, fourth, fifth, etc. coefficients x_i s respectively as k₃, k₄, k₅, etc., where k_i is a positive integer or a non-negative proper fraction, i ε { 3, 4, 5, … , m + n }, to obtain the infinite number of independent balanced forms of the chemical equation.

Application of the Novel General Procedure of Balancing Chemical Equations by Algebraic Method

In this section, the novel general procedure of balancing chemical equations by algebraic method will be employed to illustrate the said procedure by considering some examples.                   

Example 1:  Let us consider the balancing of the chemical equation:

Let the balanced equation be:

( x₁ ) NaNO₃ + ( x₂ ) Zn + ( x₃ ) NaOH → ( x₄ ) Na₂ZnO₂ + ( x₅ ) NH₃ + ( x₆ ) H₂O

where the coefficients  x_i s, i ε { 1, 2, 3, 4, 5, 6 } are smallest positive integers.

Equating the number of atoms of each element on both sides of the above chemical equation we then obtain the following equations.

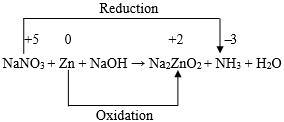
Thus, we have five equations and the number of unknown integers to be found out is six. In order to evaluate the values of the six unknown positive integers in smallest form with the help of the aforesaid five equations, we now proceed as follows.

Let x₁ = k. Then from equation (4), we get, x₅  = k.

Hence from equations (3), (5), (6) and (7) we respectively get,

Now, subtracting equation (9) from equation (8) we get, x₆ = 2k. Then from equation ( 11 ) we have, x₃ = 7k. Also from equation (8) we have then, x₄ = 4k , and from equation (10), we have,  x₂  =  4k.

Thus we obtain:

Now, x₁ : x₂ : x₃ : x₄ : x₅ : x₆ = 1 : 4 : 7 : 4 : 1 : 2.

Hence the balanced form of the chemical equation is:    

Example 2:  Let us now consider the balancing of the following chemical equation:                           

Let the balanced equation be:

( x₁ ) MgSO₄ + ( x₂ ) NaOH → ( x₃ ) Mg(OH)₂ + ( x₄ ) Na₂SO₄

Equating the number of atoms of same kind of element on both sides of the above chemical equation we then obtain the following equations.

From equations (12), (13) and (15) we get:

It can now be readily seen that both the equations (14) and (16) are satisfied with these values of x1, x2, x3, and x4.

Now, x₁ : x₂ : x₃ : x₄  = 1 : 2 : 1 : 1.

Hence, there is only one balanced form of the chemical equation under consideration and that is :

MgSO₄   +   2NaOH    →  Mg(OH)₂   +   Na₂SO₄

Example 3: Let us consider the balancing of the chemical equation:

Cr₂O7^2-  + H⁺ + Fe²⁺ → Cr³+ + H₂O + Fe³⁺

Let the balanced chemical equation be

Since the number of atoms of each kind on both sides must be equal, we have then the following equations:

Also, since the total charge before and after the reaction must remain the same, we must have,

It is important to note that the equation (21) does not contain x₅. This is only because of the fact that water (H₂O) is neutral or zero-valent.

Using equations (17) and (18), we have from equation ( 21 ),

Now from equations (19) and (20) we get,

Hence we have from equation (22), x6 = 6k. Also, from equations (17) and (18) we have then x₃ = 6k, and x₂ = 14k, respectively.

Now, x₁ : x₂ : x₃ : x₄ : x₅ : x₆    =    1 : 14 : 6 : 2 : 7 : 6.

Hence the balanced form of the chemical equation is:                               

Example 4:Let us consider the balancing of the following chemical equation:

Let the balanced form of the above chemical equation be 

Since the number of atoms of each kind on both sides must be equal, we have then the following equations:

Now, let x₁ = k₁, so that from equation (23) we have, x₄ = k₁.

Then equation (24) reduces to                                                                 

Also, equation (26) becomes

Again let x₂ = k₂, so that from equation (27) we have x₃ = ( 3k₁ − k₂ )/2.

Equation (25) then becomes   

Also, equation (28) then becomes

Now, solving for  x5  and  x6 we get from equations (29) and (30),  x₅ = ( 5k₁  −   k₂ )/2, and x₆ = ( 3k₂  −  5k₁ )/2.

Thus we have

If k₁ = 2, and k₂ = 5, we have, x₁ = 2, x₂ = 5, x₃ = 1/2, x₄ = 2 , x₅ = 5/2, and x₆ = 5/2.

Now,  when reduced to simplest form we have,  x₁ : x₂ : x₃ : x₄ : x₅ : x₆  = 4 : 10 : 1 : 4 : 5 : 5.

Thus, the balanced form of the chemical equation under consideration is :

This is the only balanced form that exists in the traditional literature.

Again for a different choice such as k₁ = 1, and k₂ = 2, we have, x₁ = 1, x₂ = 2, x₃ = 1/2, x₄ = 1,   x₅ = 3/2, and x₆ = 1/2.

Now,  when reduced to simplest form we have,  x₁ : x₂ : x₃ : x₄ : x₅ : x₆  = 2 : 4 : 1 : 2 : 3 : 1.

Thus, a second balanced form of the chemical equation under consideration is:

Let us now proceed with the choice k₁ = 5, and k₂ = 13, so that we have, x₁ = 5, x₂ = 13, x₃ = 1, x₄ = 5, x₅ = 6, and x₆ = 7.

Now, when reduced to simplest form we have, x₁ : x₂ : x₃ : x₄ : x₅ : x₆  = 5 : 13 : 1 : 5 : 6 : 7.

Thus, a third balanced form of the chemical equation under consideration is:

Proceeding in this way it is possible to obtain infinite number of independent balanced forms of the aforesaid chemical equation for all different choices of the values of k₁ and k₂.

Example 5:  Let us consider balancing of the following chemical equation:

KMnO₄ + H₂SO₄ + H₂O₂ → MnSO₄ + K₂SO₄ + H₂O + O₂

Let the balanced form be

( x₁ ) KMnO₄ + ( x₂ ) H₂SO₄ + ( x₃ ) H₂O₂ → ( x₄ ) MnSO₄ + ( x₅ ) K₂SO₄ + ( x₆ ) H₂O + ( x₇ ) O₂

Equating the number of atoms of each kind of element on both sides of the above chemical equation, we then obtain the following equations.

Now let x₁ = k₁, so that from equations (31) and (32) we respectively have, x₅ = k₁/2, and x₄ = k₁.

Then from equation (35), we also have, x₂ = 3k₁/2.

Again let x₃ = k₂, so that from equation (34), we have, x₆ = ( 3k₁ +  2k₂ )/2 and from equation (33), we have 
x₇ = ( 5k₁ +  2k₂ )/4.

Thus we have

As before, corresponding to a particular choice of the values of k1 and k2, it would be possible to get a particular balanced form of the relevant chemical equation.

For example, if k₁ = 2, and k₂ = 5, we have, x₁ = 2, x₂ = 3, x₃ = 5, x₄ = 2, x₅ = 1, x₆ = 8, and x₇ = 5.

When reduced to simplest form we have, x₁ : x₂ : x₃ : x₄ : x₅ : x₆ : x₇ = 2 : 3 : 5 : 2 : 1 : 8 : 5.

Thus, the balanced form of the chemical equation under consideration is:

This is the only balanced form of the chemical equation that exists in the traditional literature.

Again if k₁ = 2, and k₂ = 1, then it can be readily seen that, we have in this case,

Thus, the second balanced form of the above chemical equation is :

2KMnO₄ + 3H₂SO₄ + H₂O₂ → 2MnSO₄ + K₂SO₄ + 4H₂O + 3O₂

Now, if k1 = 2, and k2 = 3, then it can be readily seen that, we have in this case,

Thus, the third balanced form of the above chemical equation is :

In a similar manner, by choosing arbitrary pair of values for k₁ and k₂, it would be possible to generate infinite number of independent balanced forms of the chemical equation under consideration.

However, where multiple options for a balanced equation are possible, it is important to recognize that equalizing the numbers of electrons transferred is determinative on the stoichiometric coefficients in the least complex final balancing. For this purpose the balancing of chemical equations by the “Oxidation number method” is now being considered below with reference to the chemical equations considered in Examples 1, 3, 4, and 5 above.

For the first chemical equation, viz., NaNO₃ + Zn + NaOH → Na₂ZnO₂ + NH₃ + H₂O, the skeleton equation that includes those reactants and products containing the elements that suffer a change in oxidation numbers is as follows:

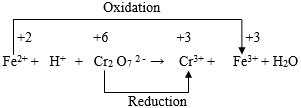
Looking at this skeleton equation we find that the oxidation number of Zn increases by (+ 2  ̶   0) or 2 and the oxidation number of N atom decreases by {(+ 5)  ̶  ( ̶  3 )} or 8.

Now, in order that the increase and decrease of oxidation number are equal, there is a need of 4 atoms of Zn and 1 atom of N. Thus, the aforesaid chemical equation may be written as follows: 

It can now be readily seen that in order to get the salt Na₂ZnO₂ as a product, there is a final need of 7 molecules of NaOH. Thus, the balanced chemical equation is:

For the third chemical equation, viz., Cr₂O₇^2- + H⁺ + Fe²⁺ → Cr³⁺ + H₂O + Fe³⁺, the skeleton equation is as follows:

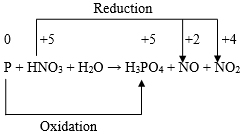
Looking at this skeleton equation we find that the oxidation number of Fe increases by {(+ 3)  ̶  (+ 2)} or 1. Again the oxidation number of one Cr atom decreases by {(+6) ̶ (+3)} or 3. Hence, the total decrease in oxidation number of two Cr atoms = 2 × 3 = 6.

Now, in order to equalize the increase and decrease of oxidation number, we are to put 2 in front of Cr³⁺, 6 in front of Fe²⁺ and 6 in front of Fe³⁺. Thus we obtain the following equation:

Now, in order to ensure that the number of O atoms on both sides are equal, the above equation will have to be changed to the following form:

The balanced chemical equation can then be obtained by equalizing the number of H atoms on both sides as follows:                                                                                                                                              

For the fourth chemical equation, Viz. P + HNO₃ + H₂O → H₃PO₄ + NO + NO₂, the skeleton equation is as follows:

Looking at this skeleton equation we find that the gain in oxidation number of P is {(+ 5)  ̶  0} or 5.

Again the loss in oxidation number of N for the conversion:

• From HNO₃  → NO is {(+ 5)  ̶   (+ 2)} or 3,
• From HNO₃  → NO₂ is {(+ 5) ̶   (+ 4)} or 1.

Thus, the net loss in oxidation number of N is (3 + 1) or 4.
Now, in order to equalize the gain and loss of oxidation number, we are to consider the following number of atoms and molecules of P and HNO₃ respectively.     

• 4 atoms of P so that the total gain in oxidation number becomes (4 × 5) or 20               
• 5 molecules of HNO₃ for the conversion from HNO₃  → NO, for which the decrease in oxidation number will be (5 × 3) or 15, the decrease in oxidation number for the conversion of one molecule of HNO₃ from HNO₃  → NO being equal to 3
• 5 molecules of HNO₃ for the conversion from HNO₃  → NO₂, for which the decrease in oxidation number will be (5 × 1) or 5, the decrease in oxidation number for the conversion of one molecule of HNO₃ from HNO₃  → NO₂ being equal to 1

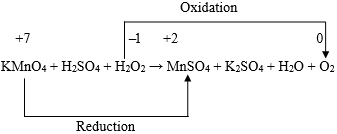
Thus, the overall loss in oxidation number will then be (15 + 5) or 20, which is exactly equal to the total gain in oxidation number.

Thus, the chemical equation under consideration can then be written as:

The balanced chemical equation can then be obtained by equalizing the number of O atoms and N atoms on both sides as follows:

For the fifth chemical equation, viz., KMnO₄ + H₂SO₄ + H₂O₂ → MnSO₄ + K₂SO₄ + H₂O + O₂, the skeleton equation is as follows:

Looking at this skeleton equation we find that the oxidation number of one oxygen atom increases by {0   ̶  ( ̶  1)} or 1. Hence, the total increase in oxidation number for two oxygen atoms = 2 × 1 = 2. Again the oxidation number of one Mn atom decreases by {(+ 7)  ̶  (+ 2)} or 5.

Now, in order to take care of the fact that the increase and decrease in oxidation number are equal, there is a need to consider 2 atoms of Mn and 10 atoms of oxygen. Thus the aforesaid chemical equation may be written as follows:                                                                                    

2KMnO₄ + H₂SO₄ + 5H₂O₂ → 2MnSO₄ + K₂SO₄ + H₂O + 5O₂

Again, to get K₂SO₄ and MnSO₄ as products, there is a need to consider 3 molecules of H₂SO₄. This ultimately leads to the balanced equation as:

2KMnO₄ + 3H₂SO₄ + 5H₂O₂ → 2MnSO₄ + K₂SO₄ + 8H₂O + 5O₂

This concludes the validity of the fact that equalizing the numbers of electrons transferred is determinative on the stoichiometric coefficients in the least complex final balancing.

Conclusion

The procedure for the algebraic method of balancing chemical equation offered in this paper is novel. At the same time it also reflects the efficiency of the algebraic method in regard to generating multiple balanced forms for some typical chemical equations. The application of this novel procedure for balancing chemical equations leads to a satisfactory answer to the fundamental fact that, the balanced form of a chemical equation is not always unique. It is definitely unique (with lowest possible integral coefficients) so long as {(m + n) – s} ≤ 1. In cases of chemical equations (not involving ions) with {(m + n) – s} > 1, and for those involving ions with {(m + n) – s} > 2, it is possible to generate infinite number of independent balanced forms of the chemical equation.

In view of all of the above, the author notes that the novel idea presented in this paper is not only mathematically interesting, but that it deserves attention from the academic and pedagogical points of view to the relevant fields of science and engineering.

References

1. Das R, Gupta BK in Physical science, 4th Edition, Oriental Book Company (P) Ltd., Calcutta, India, 1994.
2. Das R in An introduction to Chemistry, 10th Edition, Oriental Book Company (P) Ltd., Calcutta, India, 1995.
3. Maity S, Ganguly M in Elements of Chemistry, 3rd Revised Edition, Publishing Syndicate, Calcutta, India, 1997.  
4. Herndon WC. On balancing chemical equations: past and present, J. Chem. Educ., 1997, 74, 1359-1362.
5. Toth Z. Balancing chemical equations by inspection, J. Chem. Educ., 1997, 74, 1363.
6. Standen A. Some simple balancing, J. Chem. Educ., 1945, 22, 461-462.
7. Deming HG. Balancing equations algebraically, J. Chem. Educ., 1934, 11, 125.
8. Olson JA. An analysis of the algebraic method for balancing chemical reactions, J. Chem. Educ., 1997, 74, 538-542.
9. Das SC. On balancing chemical equations, Int. J. Math. Educ. Sci. Technol., 1987, 18, 746-747.
10. Swayze DR. Balancing chemical equations, J. Chem. Educ., 1963, 40, 269-270.
11. Hall WT. Balancing chemical equations, J. Chem. Educ., 1944, 21, 201-202.
12. Bottomley J. Note on a method for determining the coefficients in chemical equations, Chem. News, 1878, 37, 110-111.
13. Balasubramanian K. Linear variational Diophantine techniques in mass balance of chemical reactions, Journal of Mathematical Chemistry, August 2001, 30(2).